电子电路与系统基础(N):频率特性
先说结论:
- 数字门:延时、动态功耗
- 放大器:高频增益下降、失去有源性、变得不稳定
晶体管高频电路模型
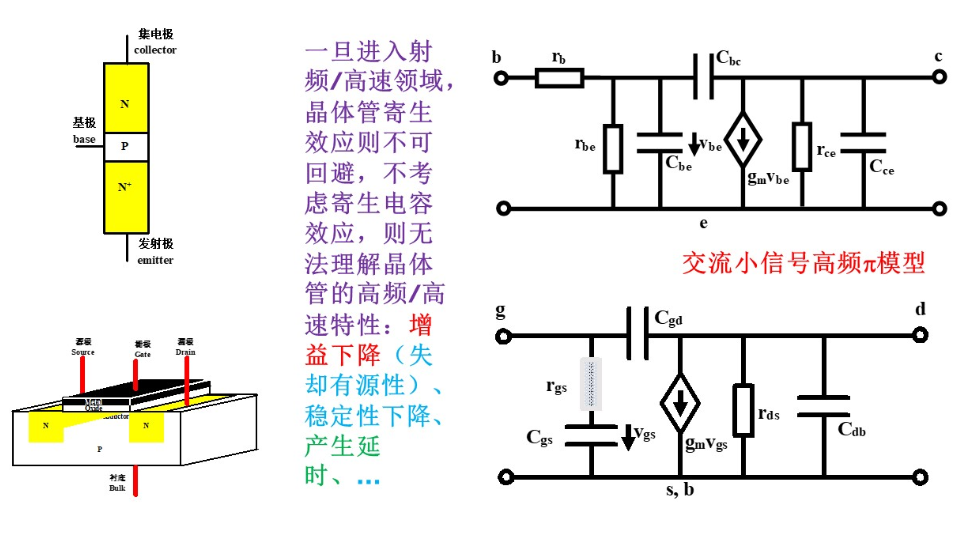
然后glgg写了一大坨公式,给我看恶心了,我们跳过这一部分。
额,深思熟虑一下至少还是写一下节点电压法的方程列写方法吧
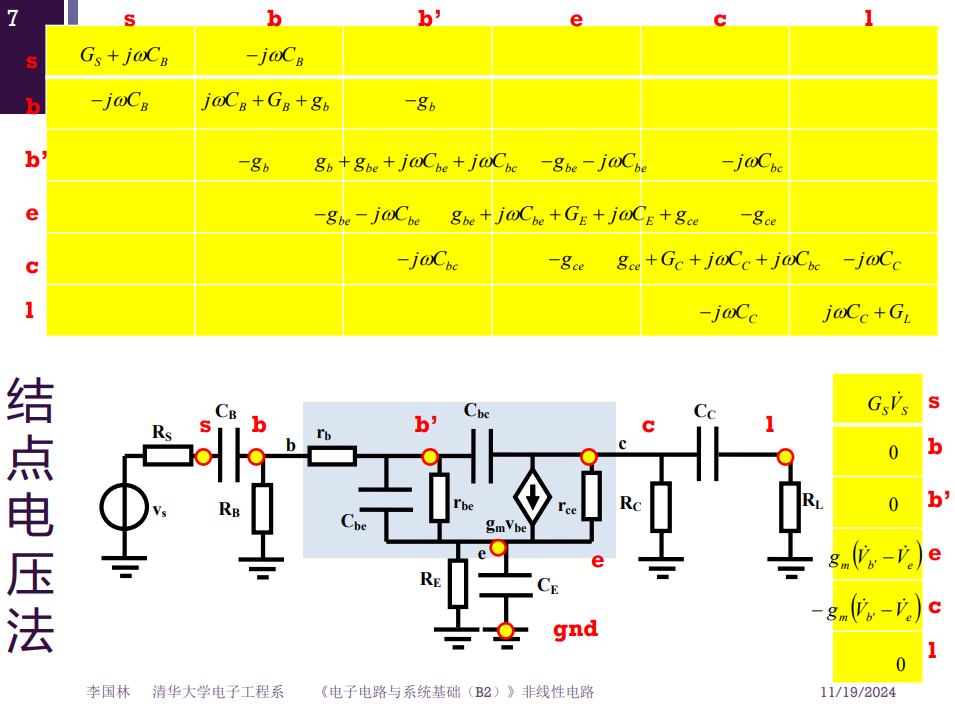
在对角线上写出直接连接到该节点的导纳之和,然后其他地方写直接连接两个节点的导纳之和的负值
然后向量里面写通过源流入该节点的电流
然后就可以愉快的用Matlab来算这一坨了!
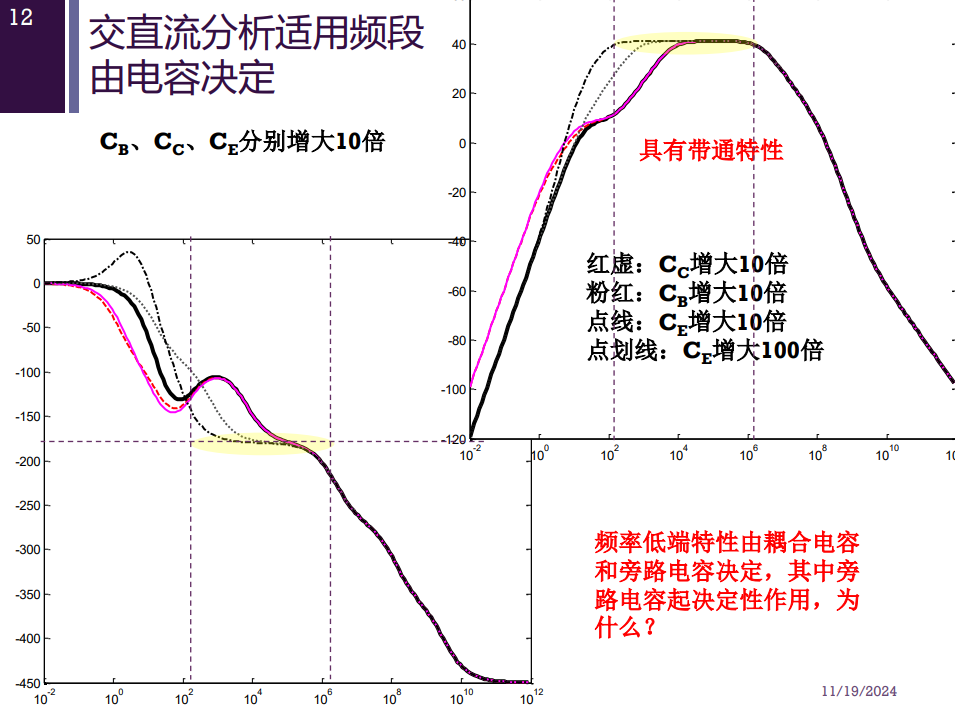
感性分析一下
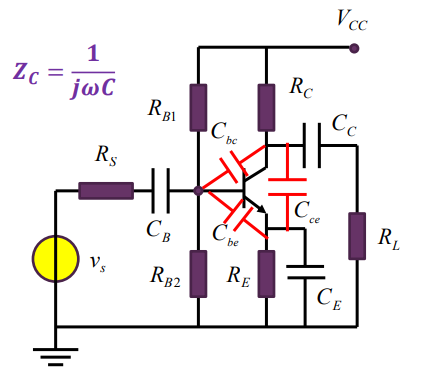
首先是频率极小的时候,三个寄生电容特别小,认为是开路的,不产生影响。但是都开路了,开路使得输入信号传不过来,开路使得输出信号传不出去,开路使得交流信号通过负反馈电阻,减小了增益。
然后是频率极大的时候,人为设置的三个外围电容短路,正常传递交流信号,但是短路了,信号直接接地了,而且三极管组成的跨导器失去了控制作用,所以增益变小了
定量粗分析
分析五阶电路多少还是太悲惨了,所以我们粗略分析一下电路的频率特性
低频端近似分析
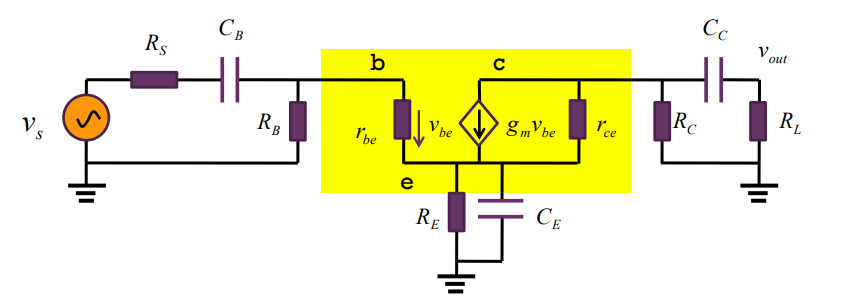
比较小,我们直接忽略,同样被忽略掉的还有三个寄生电容
然后我们再来单独分析三个外围电容
输入耦合电容的影响
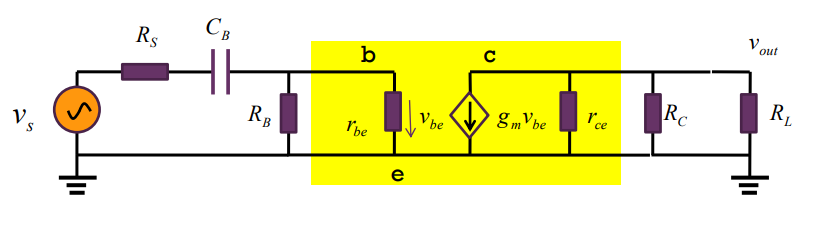
他具备典型的高通传递函数,所以我们直接写答案
其中可以视作高频短路时候的增益,直接可以写出来
则是输入耦合电容的时间常数,
输出耦合电容的影响
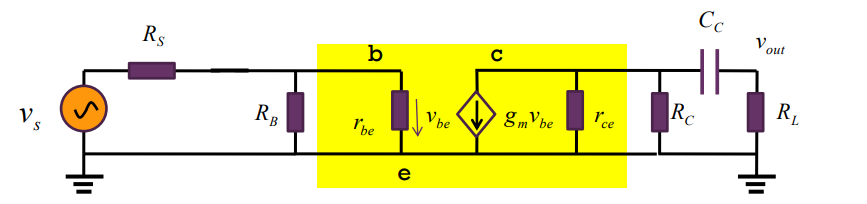
同样是高通传递函数,直接写答案
TODO:稍微写一下
旁路电容的影响
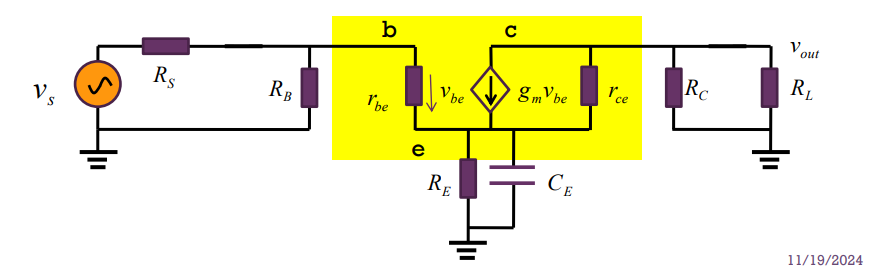
我操,这个难,
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.