电子电路与系统基础复习（1）二端口网络参量：一切故事的开始

网络参量的引入

对于一个电路系统来说，最朴素的认知是认为系统分别有输入输出两个端口，因此对二端口网络的描述是最为重要并且基础的。
我们所能直接测量的无非网络的电流和电压，两个端口也就是两组电流和电压，对于线性网络来说，我们很容易能够列出来四个变量组成的二元一次方程组
比如对如图所示的二端口网络，我们可以列出如下的方程组

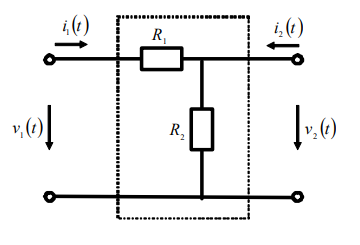
$$v_1 = (R_1+R_2)i_1 + R_2i_2 \\\\ v_2 = R_2i_1 + R_2i_2$$

矩阵形式也就是

$$\begin{gathered} \begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} = \begin{bmatrix} R_1+R_2 & R_2 \\\\ R_2 & R_2 \end{bmatrix} \begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} \end{gathered}$$

那么不妨就将上面的矩阵作为网络的的一个描述，以此我们得到了二端口网络的z参量描述

$$\begin{gathered} \begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} = \begin{bmatrix} z_{11} & z_{12} \\\\ z_{21} & z_{22} \end{bmatrix} \begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} \end{gathered}$$

类似的我们还有其他种类的参量

$$\begin{gathered} \begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} = \begin{bmatrix} y_{11} & y_{12} \\\\ y_{21} & y_{22} \end{bmatrix} \begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} \end{gathered}$$

$$\begin{gathered} \begin{bmatrix} v_1 \\\\ i_2 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} \\\\ h_{21} & h_{22} \end{bmatrix} \begin{bmatrix} i_1 \\\\ v_2 \end{bmatrix} \end{gathered} \space \space \begin{gathered} \begin{bmatrix} i_1 \\\\ v_2 \end{bmatrix} = \begin{bmatrix} g_{11} & g_{12} \\\\ g_{21} & g_{22} \end{bmatrix} \begin{bmatrix} v_1 \\\\ i_2 \end{bmatrix} \end{gathered}$$

$$\begin{gathered} \begin{bmatrix} v_1 \\\\ i_1 \end{bmatrix} = \begin{bmatrix} A & B \\\\ C & D \end{bmatrix} \begin{bmatrix} v_2 \\\\ i_2 \end{bmatrix} \end{gathered} \space \space \begin{gathered} \begin{bmatrix} v_2 \\\\ i_2 \end{bmatrix} = \begin{bmatrix} a & b \\\\ c & d \end{bmatrix} \begin{bmatrix} v_1 \\\\ i_1 \end{bmatrix} \end{gathered}$$

上面的参量依次被称为阻抗参量，导纳参量，混合参量，混合参量，传递参量，逆传参量。
他们具有以下的等效电路

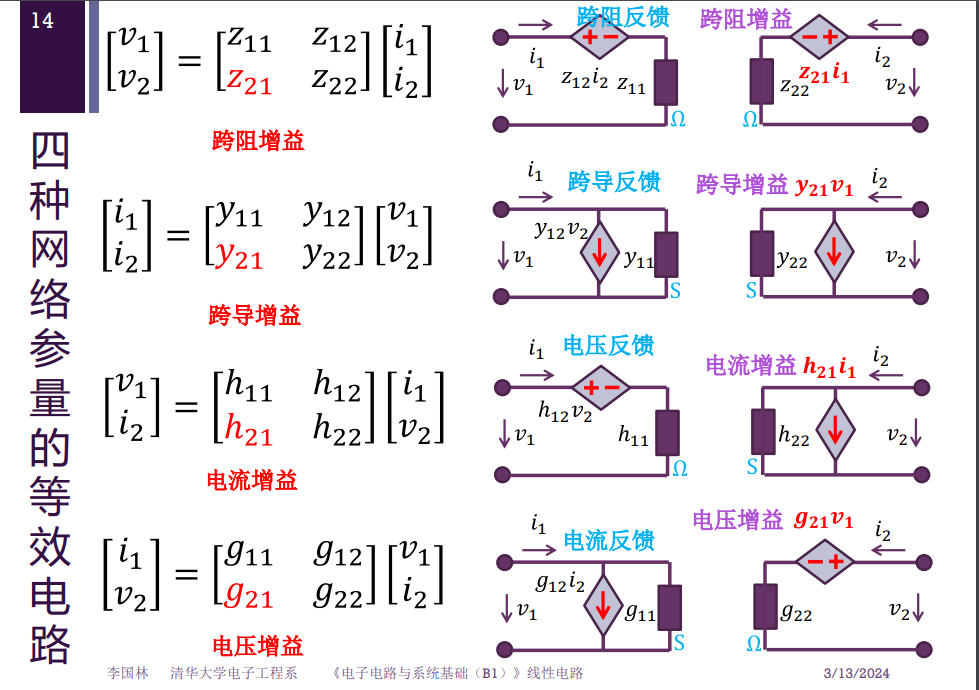
其中每个矩阵中下标为21的项都可以视作从输入到输出的增益，如上图所示。
对于参量的求取有下面的规则

传输参量要特殊一些，ABCD四个参量的倒数为端口1到端口2的四个本征增益（传输矩阵直接表示从输入端口到输出端口的关系，所以是“本征”）
下面是我最喜欢的一张图，当初课上引起一番轰动

这里是比较重要的计算规则

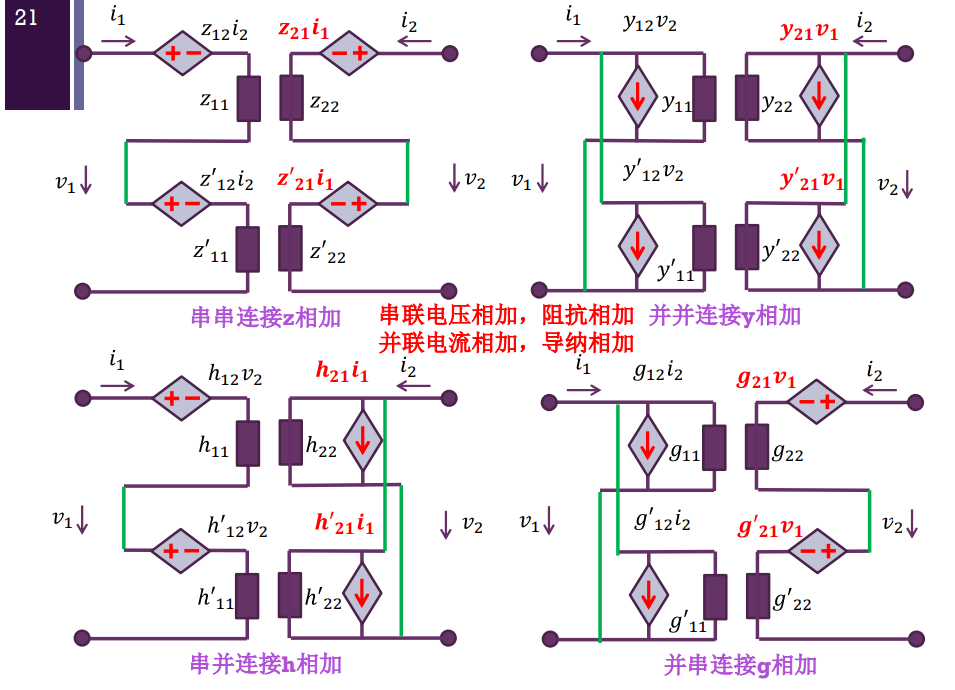
级联的话则是ABCD矩阵相乘（简单的线性代数知识）
现在我们对网络参量有了一个基本的概念，下面要通过网络参量的方法来分析电路系统的性质。
TODO:第五讲PPT,回路电流与节点电压法